PHYSICO MATHEMATICAL INTERPRETATION OF THE PHARMACOLOGICAL EFFECT OF HIGH DILUTIONS : REMANENT WAVE, CONTONIAN APPEARANCE (conton)

Henri BERLIOCCHI, Rolland CONTE 7° Symposium du GIRI, Montpellier 20-21 Novembre 1993

For the interpretation of the hormesis curves we are introducing a new statistics: the contonian statistics. The underlying mathematical theory of this statistic is the theory of Ethers. This theory is not probabilistic but introduces a problematic of indecidability. The physical frame concerned is related to the quantum theory of fields, the central problem of which lies in the construction of a field that is solved by using the theory of Ethers.

The model used for the physico-mathematical interpretation of the pharmacological effect of high dilutions is as follows: the second quantification is considered for a free material particle (which is the basis of the quantum theory of fields, the current theory in physics covering matter-light interactions) in space-time, the field being calculated with the usual methods applied by physicists (renormalization) through the integral of Feynman. The theory of Ethers allows then, what was so far impossible, to fully justify the calculations from physicists in this frame and, furthermore, to consider other frames since the calculations are mathematically validated. The usual frame is shown in Figure1. The mass (M) is uniformly spread in the space-time, this means homogeneously.

We imagine a different frame, shown in Figure 2. We consider the mass as being non uniformly spread, and non existing in the cone of the future of a point. Within this frame, the mathematical calculation shows, in the cone of the future where the particle has disappeared, the apparition of a non trivial physical field having the same unit as the electromagnetic field: we call this field the remanent wave. The word remanent is already used in magnetism (magnetization of iron in a magnetic field).

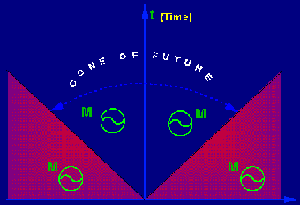
From this approach, we have a complete mathematical frame for the analysis of this remanent wave and for the examination of the possible irradiations effects it can produce to the surrounding remaining matter (for example the substrate of a homeopathic drug). Of course, at this stage, it is only a model (we take into consideration only the "mass" character of the particle when other characters exist as well). However, a possibility to enjoin the experimental approach exists throughout contonian statistics and the conceptual frame in which the remanent wave is represented in the form of contons is therefore well founded.

For the definition of the contonian appearances (contons) the following method is used. From the remanent wave, products called chronological are built and then "read" via the help of a character (contonian appearance). By doing so, the contons are obtained. In practice, a conton is defined as an appearance of a dynamic system, general mathematical notion that summarizes the approach of any type of evolutionary system. When using this modeling, the principle consists in considering the space of the" states" of the system, that means all possible values of the parameters of the system, and in defining a dynamic system as a way to pass from one state to another one. More information on the general definition of the conton are given in the book : "Nouvelle Economie Théorique" (Conte and al., 1993) (1).

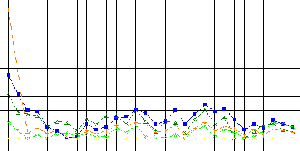
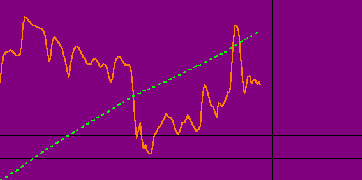
We will now describe the practical methods that allow to "read" a contonian phenomenon and, for doing so, we will consider hormesis curves. Let v be the parameter we will call Hahnemannian parameter whose usual units are CH or DH. We observe a quantitative character x(u) that can be very various (optical density, death rate of a batch of mice,...) and by using the method of the trapezes we calculate the integral that is expressed as follows:

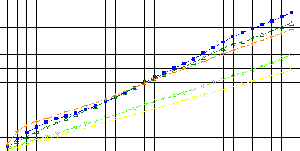
Int (vo, v) x(u)du = L(v)

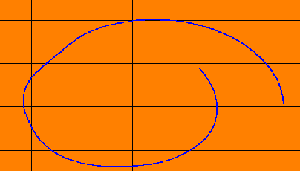
This integral will be the contonian lagrangian, so called because its typology is the same as the optic path in physics. The aspect of the curves L(v) will be linear. We can calculate the contonian frequency H, since the conton is defined by the relation:

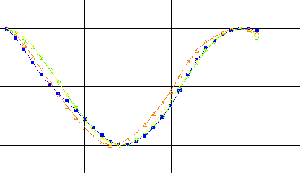
exp(i H Int (vo, v) x(u)du

and represents the point of the circle that varies as a function of the Hahnemannian parameter according to a circular movement:

Teta= H Int (vo, v) x(u)du

Teta being the polar angle of a point of value equal to the v parameters. The Euler’s relation allowing the expression of an exponential in the complex plane is illustrated in Figure 3. The second step of the practical construction of a conton consists in adjusting the constant H in order to get, in the complex plane, a continuous trajectory. The H value so determined is called the contonian frequency. A dedicated software, used for the analysis of the experimental results and that will do the operations described in the above methodology, is under development (*). By using this methodology and/or this software it is then possible to verify the action of the infinitesimal dilutions.

To illustrate the results gotten with this new statistics, we chose contons deriving from other fields such as rainfall, geodesy, economy, physics in nuclear magnetic resonance and infra-red absorption.

Figure 4 presents the sum of the rainfall data of 66 ONM French stations (ONM = National Meteorological Office ) as well as the related lagrangian values. We draw the reader's attention to the almost linear aspect of this lagrangian, aspect that is characteristic of the contonian processes.
(*) Software: Analyse Activité Pharmacologique Dilutions Infinitésimales

Figure 5 shows, for the contonian frequency H, the variation of Cos (H*L(v)) that means the real part (Re) and the one of Sinus (H*L(v)) that means the imaginary part (lm), according to the time. When we have at our disposal enough contons related to a same phenomenon, for example related to N rainfall curves (or to N hormesis curves), we say that we are in presence of a Feynman’s sample and then, we can practice the contonian aggregation, that is to say the superposition of the contonian phases.

Figure 6 shows the curve gotten by this technique for the 66 ONM French stations. This curve is remarkably spirally as foreseen by the law of the large contonian numbers. For the contonian phenomena, we always observed this shape that shows that the samples are definitely samples in the Feynman’s meaning and that the underlying dynamic systems have a global behavior of a one parameter group.

In the economic field, to illustrate the assessment of a contonian price index, we calculated, monthly, the contonian lagrangian and determined the contonian frequency for each of the 55 constituents of the American price index, the Consumer Price Index (CPI). All these prices vary with time. For example, for gas, an important monthly fluctuation of the price at the gas station occurred during the considered period (from 1980 to1991).

In spite of this, we definitively observe the linear shape of the contonian lagrangian as shown in Figure 7.

The spiral characteristic of a Feynman’s sample presented in Figure 8 is gotten by the contonian aggregation of the 55 articles constituting the CPI. The contonian aggregation would, for example, permit to aggregate results of a test of isotherapics on a sample of population.

During our research of contonian processes in the nature, we analyzed measures gotten with the sensors recording the seismic movements. As shown in Figure 9, the spectrum of the measures recall the rainfall curves and the lagrangians corresponding to the night and day measures are almost linear.

Figure 10 shows the evolution of the contonian phases according to the time. We won't debate in detail the consequences of the difference between the day and the night. However, this modification of the phase of the earth in a given point could influence the behavior of organisms treated with infinitesimal hahnemanian dilutions.

We can imagine some interactions between the remanent wave and the variation of the phase in a given point of the earth. In the chosen examples the contons were temporal, that means that the time was taken as reference of the phenomenon. In the following examples we will take the hahnemanian parameter (CH or DH) as basis of the conton. The setting in evidence of the remanent wave (Figure 11) appears very clearly on Nuclear Magnetic Resonance (NMR) measures. The example that illustrates the contonian behavior of the relaxation time T2 according to the hahnemanian parameter is relative to the nitric acid (Lasne, 1993) (2).

This Figure shows the characteristic aspect of the NMR signals that fluctuate according to the Hahnemanian parameter that varies from 1 to 60 CH. The integral of this signal is remarkably linear with a coefficient of determination R2= 0,999974. The lagrangian of the nitric acid is higher than the one of the water (non succussed). The respective contonian frequencies are: H1 = 8,384 * 10-5 for the nitric acid and H2 = 1,0667*10-4 for the non succussed water. The ratio of the contonian frequencies gives the coupling between the succussed nitric acid and the  water. This ratio is of 0,786.

Figure 12 shows the evolution of the hahnemanian contonian phases according to the hahnemanian parameter that varies from 1 to 60 CH. The phase displacement of the non succussed water appears clearly. Besides, the contonian frequencies of the nitric acid and of the water are different, the nitric acid disappearing progressively in the medium but being still represented by its remanent wave. These two elements behave like two different notes of music, each of them having its own frequency.

This experience, whose reproducibility of the results has been demonstrated by other series of experiences, permitted to determine a parameter H that has also been calculated on another series of measures (another distinct experience).

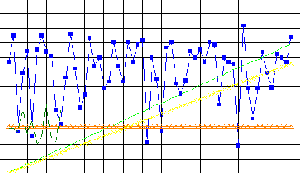
The gap between these two values of H is about 2% and within the margin of error for this type of measures. This confirms the interpretation by the remanent wave of the activity of the high dilutions. Indeed, the theory foresees that the parameter "contonian frequency" is a data that only depends on the substance put in solution, here the nitric acid, so long as the same source of water is used for dilutions in order to eliminate the effects due to the residual impurities of this water or that one makes sure, for every source of water, that the parameter measured for the first source of water remains unchanged. The observed phenomenon is really due to the remanent wave, that is to say to the radiation of a " white hole" left by the disappearance of the matter in solution. This phenomenon is located at the level of the nucleons of the solution as shown by Y. Lasne who measured the T2 parameters of the ion H+ become " super proton" by the action of the remanent wave and of the ion O17H - also modified by the remanent wave. A phenomenon of remanence exists effectively when matter disappears, that means a certain form of "memory", but this concerns the memory of the emptiness, if one must take a vivid expression, and we are going to see that this same phenomenon of remanence is observed for non-aqueous solutions. We will simply point out that the theory due to J. Benveniste and his team, theory that the polemic translated by the setting in evidence of the" water memory”, doesn't permit to interpret the remanence correctly. According to this theory, the "memory", would be due to a modification of the water dipole by the substance in solution. This theory is based on the physico-mathematical calculation developed by Del Guidice (Del Guidice and al, 1988)(3) that supposes that at least a molecule of the initial substance still remains, what is not the case when we passe the 12 CH. Besides, this physico-mathematical interpretation has the inconvenience to make appear the same type of field before and after the succussion, what is not verified by the experiences achieved by Y. Lasne in NMR.

This phenomenon of remanence of the non-aqueous solutions has also been observed by Samuel Hahnemann who showed that, if gold or silver in their natural state have no action on man, their infinitesimal dilutions in another solid invest them with other properties: "... from the grinding continued during one hour of a gold grain with hundred grains of lactose in powder, results a preparation that already has a lot of medicinal virtues. If one continues to act until every grain of the ultimate preparation contains a quadrillionth (10-24) of gold grain, then we will have a medicine, in which the medicinal virtue of gold will be so developed that it will be sufficient to take one grain, to store it in a small bottle and to give it for breathing during some instants to a melancholic, to whom the disgust of life is pushed up to the point to lead him to the suicide, so that, one hour after, this poor wretch is delivered of its bad demon and recovers the charm to life. (4).

The last illustration of the contonian behavior is relative to an older publication from Heintz (Heintz, 1941) (5) on the infra-red absorption by solutions diluted n tenfold and succussed. In this article, we have selected the solutions studied with the same wavelength of 7,1 microns and having the same initial concentration of D1 = 0,1. The selected products are sodium nitrate, hydrazine and acetic acid.

Figure 13 shows the variations of the raw signal measured by Heintz according to the Hahnemanian parameter expressed in D H. The graph obtained shows a certain analogy between the signals of the three compounds studied. One notes that, qualitatively, when the non succussed water corresponds to the lowest value of the signal, intensities are increasing from hydrazine to sodium nitrate via acetic acid.

Figure 14 shows the lagrangians of the raw measurements of the signal. Although the measurements have been taken from the Heintz publication, the lagrangians are almost linear, the lagrangian of the water having the lowest slope. As for the other examples presented, we have determined the Hahnemanian contonian frequencies for these products, each product having a specific frequency.

Figure 15 shows the evolution of the contonian phase expressed here by the variation of its cosine as a function of the succussion level. This representation shows for sodium nitrate, hydrazine and non succussed water, the identity of the shape of this phase as foreseen by the contonian statistics. One notes a slight phase displacement for the acetic acid. However, when transferring this curve, it superimposes the three others. We draw the attention of the reader to the fact that, although these signals superimpose, they correspond to frequencies that are specific for each compound (H values indicated in Figure 15).

Starting from these raw data, that were not very usable, contonian statistics allows to put in evidence the fundamental parameter that drives the phenomenon.

Figure 16 represents the variations of the hahnemanian contonian period that is, in fact, the inverse of the frequency according to the molecular mass of these products. This representation shows clearly that the hahnemanian contonian period increases with the molecular mass. Finally, we want to insist on the fact that the contonian phenomena are not "uncertain" phenomena or "random" phenomena as said in scientific jargon.

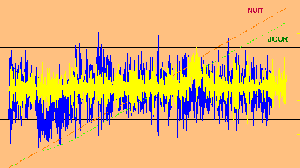
Their statistics is interpreted in the Theory of Ethers and is not a probabilistic statistics as already said while beginning this presentation. A typical example of random phenomena, the white noise or Brownian movement, is not contonian. A contonian process has an"informational" content that the white noise, that " forgets" its past, doesn't have, and its" memory" has the same nature that the one of light (electromagnetic waves): the light from the stars keeps, after millions, or even billions light years away, the information of the matter of the periphery of the star.

The illustration of the contonian behavior of the high dilutions effect has been tackled by M. Bastide and col. on a model of Candida albicans pre-treated with the 5FC at different CH. Other experimentations are in progress in the toxicological field that should allow us to generalize this mathematical interpretation to other contonian characters such as mortality for example. The illustration of the contonian behavior of the high dilutions effect brings us to recall two major ideas of Hahnemann. In page 275 of the book already quoted, Hahnemann expresses as follows his 2nd natural law "A stronger dynamic disease extincts, in a lasting manner, another less strong dynamic disease in the living organism, when the first looks like the second as for the species."

These are in fact the white holes that, while combining with the black holes (the" toxic") lead to a resultant specter that goes from the disappearance of the black holes (Pi phase displacement) to super black holes (nil phase displacement ) while going through the formation of holes having all nuances of gray. It is this resultant that will interact with the organism and will produce the observed effects. Let's recall that, in astronomy, one calls "black hole" a region of the space-time having an infinite density of matter. The region where are localized the nucleons behaving locally in this way, we used this terminology. We also recall that, for Hahnemann "the medicinal substances are not dead matters; their real nature is dynamic: it is a pure strength".

This mechanism, that has been illustrated by Yves Lasne by the interaction between a hahnemanian dilution and peroxydases, has to be brough closer to another idea already expressed in these terms by Hahnemann in page 276 of the quoted work:"the organism, as a living unit, cannot admit two similar dynamic diseases at the same time without the weakest being oblige to give way to the strongest. However, since it tends to be affected more strongly by a medicine than by an analogous illness, this one must necessarily leave it, and he is then cured". In fact, it is the "Nature" and no the organism that cannot admit the coexistence of two " similar dynamic disease". There is an interaction between the phases of the white and black holes. When these phases are opposed, their interaction leads to a nil resultant and the patient is cured.

Acknowledgments:

We are pleased to thank the personalities who helped us in this survey and more particularly Mr. P. Dorfman of the Dolisos Laboratory, Mrs. Professor Madeleine Bastide, Mr. Professor J. Cambar and Mr. Y. Lasne for their attitude and the enthusiasm they testified to undertake some experiences or "to search" in their laboratory notebooks in order to extract some experimental results.

Bibliography
1.	CONTE (R.R), BERLIOCCHI (H), ANDRAS (H.G.) : Nouvelle Economie Théorique. Editions Economica, Paris, 1993
2.	LASNE (Y.) : L'homéopathie de/par l'information De Natura Rerum, 1993,7,pp 95-168
3.	DEL GUIDICE (E), PREPARATA (G.), VITTELLO (G.) : Water as a free electric dipole laser. Phy. Rev. lett., 1988, 61, pp 1085-1088.
4.	HAHNEMANN (S.) : Etude de Médecine Homéopathique, première série. Editions J.B Baillière, Paris, 1855, p.579.
5.	HEINTZ (E.) : Physikalische Wirkungen Hochwerdünnter potenzierter Substanzen Die Naturwissenschaften, 1941, 29, pp.713-725.